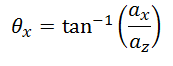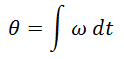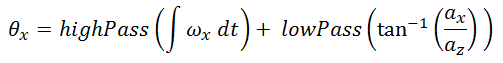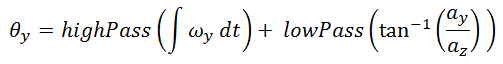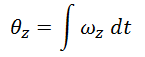Difference between revisions of "S14: Tricopter"
Proj user2 (talk | contribs) (→Testing & Technical Challenges) |
Proj user2 (talk | contribs) (→Phase #2) |
||
| Line 300: | Line 300: | ||
=== Phase #2 === | === Phase #2 === | ||
| − | Following the verification of the the electrical components, rudimentary flight and motor control tests began. During this phase no propellers where attached to the motors due to safety concerns. The main objective was to fully comprehend the correlation between motor speed and pulse width percentage. It was during this phase that the team encountered issues with the included PWM class. The issue and solution was documented in [Issue #2]. | + | Following the verification of the the electrical components, rudimentary flight and motor control tests began. During this phase no propellers where attached to the motors due to safety concerns. The main objective was to fully comprehend the correlation between motor speed and pulse width percentage. It was during this phase that the team encountered issues with the included PWM class. The issue and solution was documented in [[Issue #2]]. |
=== Issue #1 === | === Issue #1 === | ||
Revision as of 21:47, 21 May 2014
Contents
- 1 Grading Criteria
- 2 Code name Cerberus
- 3 Abstract
- 4 Introduction
- 5 Objectives
- 6 Schedule
- 7 Parts List & Cost
- 8 Design & Implementation
- 8.1 Hardware Design
- 8.2 Hardware Interface
- 8.3 Software Design
- 8.4 Orientation
- 8.5 Motor Control
- 8.6 Balancing Algorithm
- 8.7 Fail safe
- 9 Testing & Technical Challenges
- 10 Conclusion
- 11 References
Grading Criteria
- How well is Software & Hardware Design described?
- How well can this report be used to reproduce this project?
- Code Quality
- Overall Report Quality:
- Software Block Diagrams
- Hardware Block Diagrams
- Schematic Quality
- Quality of technical challenges and solutions adopted.
Code name Cerberus
Abstract
The goal of this project is to produce a stable hovering tricopter. This craft will hover using three motors with three propellers, one of which is mounted on a swivelling piece that allows the raft to have more yaw control. The plan for this project is to use COTS parts for all but the flight controller which will be our software on an SJOne board. The flight controller is responsible for determining how fast each motor spins and the angle of the swivelling motor using inputted data from an accelerometer, a gyroscope, and possibly a magnetometer. The tricopter will elevate itself to a fixed height and using a barometer will stay stabilized at this height.
Introduction
Multrirotor unmanned arial vehicles (UAV), have recently grown in popularity due to the reduced cost in parts. A highly agile variation of these multirotor copters are the tricopters. Tricopters apply equivalent principles of balance and orientation to that of traditional multirotors. Unlike symmetrical multirotors, tricopters require an additional servo to counteract yaw. Roll is controlled exclusively by the front left and right motors, where pitch is adjusted through a combination of all three.
Objectives
The objective of this project is to produce a Tricopter capable of rising to a given altitude, hovering in one position for at least 15 seconds, and then landing safely in the same position it took off from.
Maintaining stable flight is the key requirement for this project. Orientation is calculated using an accelerometer and gyroscope. The height above ground is determined using the output of an ultrasonic sensor.
Team Members & Responsibilities
- Carlos Fernandez-Martinez
- Shane Loretz
- Michael Schneider
Schedule
Show a simple table or figures that show your scheduled as planned before you started working on the project. Then in another table column, write down the actual schedule so that readers can see the planned vs. actual goals. The point of the schedule is for readers to assess how to pace themselves if they are doing a similar project.
| Week# | Date | Task | Actual |
|---|---|---|---|
| 1 | 3/21 | Create schedule | Delayed due to wiki-login issues |
| 2 | 3/28 | Build Tricopter frame, establish PWM communication | Completed, PWM driver had to be replaced |
| 3 | 4/4 | Establish connection with IMU, create an orientation task | Completed, no issues encountered |
| 4 | 4/11 | Complete the wiring of the frame, build power regulator for 5v | Completed, regulator circuit unneeded, ESCs provide adequate power |
| 5 | 4/18 | Integrate motor control task with orientation task | Completed, no issues encountered |
| 6 | 4/25 | Balancing and orientation test | In progress |
Parts List & Cost
Give a simple list of the cost of your project broken down by components. Do not write long stories here.
| Name | Quantity | Price |
|---|---|---|
| Turnigy Park480 | 3 | $61.47 |
| Hobby King 30A ESC | 3 | $30.45 |
| Corona 919MG Servo | 1 | $7.01 |
| Sunkee 10DOF | 1 | $20.00 |
| Hobbyking X900 | 1 | $32.16 |
| Prop 9047 | 3 | $9.48 |
| Truningy 5800mah | 1 | $27.85 |
| Cables / Connectors | N/A | $20.00 |
| SJSU One Board | 1 | $80.00 |
| Total | $292.00 |
Design & Implementation
The design section can go over your hardware and software design. Organize this section using sub-sections that go over your design and implementation.
Hardware Design
Discuss your hardware design here. Show detailed schematics, and the interface here.
Hardware Interface
In this section, you can describe how your hardware communicates, such as which BUSes used. You can discuss your driver implementation here, such that the Software Design section is isolated to talk about high level workings rather than inner working of your project.
Software Design
The software uses two FreeRTOS tasks: the orientation task and the motor control task. The orientation task runs every 5 milliseconds and retrieves sensor data from the accelerometer, gyroscopes, and height sensor. It uses this data to calculate the current orientation. The result is packed into a structure and pushed onto a queue of size 1. The motor control task feeds off this queue every 20 milliseconds. It uses the orientation to calculate motor speeds. The motor control task contains the balancing algorithm and fail safe condition checking.
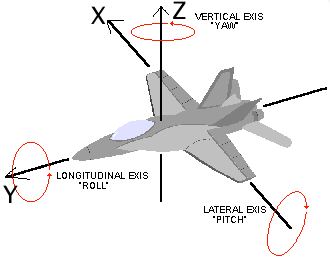
Orientation
The orientation is calculated with a combination of the accelerometer and gyroscope readings.
Orientation is expressed in radians from a level position
| X (roll) | Y (pitch) | Z (yaw) | |
|---|---|---|---|
| Positive | Rolled left | Pitched down | Yawed counter clock wise |
| Negative | Rolled right | Pitched up | Yawed clock wise |
Angular velocity is specified in radians per second
| X (roll) | Y (pitch) | Z (yaw) | |
|---|---|---|---|
| Positive | Rolling left | Pitching up | Yawing counter clock wise |
| Negative | Rolling right | Pitching down | Yawing clock wise |
Accelerometer
The accelerometer readings give the instantaneous acceleration. When the accelerometer is not moving, the only acceleration comes from gravity. If the device is flat, the entire gravitational acceleration is in the vertical (Z) component of acceleration, as shown below:
<<pic flat acceleration>>
The accelerometer reading in this instance would be <0g, 0g, 1g>, where g ~= 9.8m/s^2. However, if the accelerometer is not flat, the gravitational acceleration splits into both horizontal and vertical components, as shown below:
<<pic tilted acceleration>>
With simple trigonometry, the angle that the accelerometer is at can be calculated using these two components and an inverse tangent function:
Gyroscope
The gyroscope readings give the angular velocity. To calculate an angle, these readings can be integrated:
However, these readings are subject to "drift", where they do not return back to 0 due to small errors in the integration process.
Orientation Calculation
The solution to both of the accelerometer and gyroscope shortcomings is to filter and combine them. The accelerometer data can be trusted in the long term, since it is accurate when the craft is stable. Therefore the accelerometer data is low pass filtered. The gyroscope data can be trusted in the short term, since it is accurate when the craft is moving. Therefore, the gyroscope data is high pass filtered. The two are then combined to produce a fairly accurate orientation value.
The accelerometer cannot give any acceleration data for the Z (yaw) axis, so the orientation is only calculated using the integral of the gyroscope data. In testing, this proved to be accurate enough for our uses since the craft does not yaw significantly.
Motor Control
Motor speeds are increased and decreased to get back to an orientation of (0,0,0) (level flight). The motors are controlled by electronic speed controllers (ESC's). These take a servo PWM signal as input and use the pulse width to control the speed of a 3-wire brush-less motor. The tricopter has three motor/ESC pairs. The tricopter also has a servo which takes the PWM signal directly
| Motor 1 | Front left |
| Motor 2 | Front right |
| Motor 3 | back (with servo) |
Each motor is controlled by setting a percentage. 0% is the lowest speed, and 100% is the highest speed. Each motor's speed is set by adding a baseMotorPercentage with the motor's specific correction. The base motor percentage is used to set the throttle of the tricopter, while the correction terms are used for balancing. The base motor percentage was intended to be set by the term height_output. This was intended to control how high the tricopter would fly. Unfortunately our balancing algorithm takes too long to stabilize to allow for flight, so when balancing on the stand the base motor percentage is set to a fixed value: 20%;
Balancing Algorithm
We came up with many algorithms while working on this project. They can be divided into two families: the first are all algorithms that adjusted motor speeds based only on our current orientation, and the second are all algorithms that adjusted motor speeds based on our angular velocity and our orientation.
Algorithm type 1: Adjusting motor speeds in response to just our orientation
Accumulating motor speed to target orientation
One of the earliest algorithms we tried was extremely simple. It Increased or decreased motor speeds by a fixed amount based on the current orientation. While the craft was rolled right, it would increase the front right motor and decrease the front left motor by a fixed amount. The same was implemented on the pitch axis.
This algorithm resulted in a thrashing behavior. One motor would wind up and tilt the craft quickly. While the craft was rolled right, the right motor speed would be increasing quickly. The roll angular velocity would increase until the craft was rolling left, but as long as it was still rolled to the right, the velocity at which it rolled left would continue to increase. This caused it to over shoot the target orientation. This process repeated itself and the tricopter would continue to thrash back and forth.
Fixed motor speed adjustments to maintain orientation
Another algorithm we tried in this family relied on knowing what motor percentages were needed for the craft to hover normally. We tested the tricopter on the ground and adjusted the motor speeds until it just lifted off. We hard coded these values in our algorithm.
We used these values in our balancing algorithm as the normal motor speeds. Increasing height was done by increasing the motor speeds by a fixed amount. If the craft was rolled right, the left motor would be decreased by a fixed amount from the hover value and the right motor would be increased by a fixed amount. The same was done on the pitch and yaw axes.
This algorithm also did not work. It has some obvious problems. The craft would still overshoot the target orientation because the fixed adjustments were the same at all orientations no matter how great or small. Our hover motor speeds were inaccurate, and didn't account for ground effect. Closer to the ground our motors generate more lift, so the motor speeds are smaller to maintain hovering. The motor speeds also did not differ by a fixed amount. At higher speeds, the difference between motor speeds to maintain level flight was much higher than at lower speeds.
Change motor speeds that scale based on how far off the orientation is
This is an important concept that is used in our final balancing algorithm. Variations of the above algorithms were tried that scaled the corrections to the motor speeds based on how far off the orientation was. When our orientation was just a little off, our corrections would be smaller. This still did not solve the fundamental problem with this family of algorithms. By targeting orientation only, our angular velocity went unchecked. We would still overshoot our target orientation and get an oscillating or thrashing behavior.
Algorithm type 2: Adjusting motor speeds in response to orientation and angular velocity
This family of algorithms divides balancing into two steps. The first step used current orientation to create target angular velocities, and the second step compared our actual angular velocities to our target angular velocities and adjust the motor speeds until to make them match. Three angular velocities were considered: roll, pitch, and yaw. Our actual velocities come from the gyroscope and are converted to radians per second before they are used.
Our target velocities were set depending on our current orientation. We tried different variants just like the type 1 algorithms. We tried setting the target angular velocities to fixed values depending on our current orientation. Later we tried setting our target velocities based on the magnitude of our orientation error. This concept is what we stuck with.
We tried many different ways of adjusting our motor speed based on our target and actual velocities. They can be divided into the next two groups
Setting motor speeds based on the difference between target and actual angular velocities
We tried setting our motor speeds directly based on the difference between our actual and target velocities. If we were rolled right our target_roll would be set to rolling left at a speed depending on our orientation. While our actual_roll was not rolling left as fast as our target specified, our front right motor correction would be set to a higher value and our front left value would be set to a lower value depending on the magnitude of the error between the actual and target angular velocity.
Increasing and decreasing motors speeds based on angular velocity differences.
The next variant of the type 2 algorithms accumulated motor speeds by amounts that depend on the magnitude of the error between the target and actual values. While the actual_roll was less than the target roll, the motor speeds would be incremented by an amount that scaled with the error.
PID control of motor corrections
At this point in the project we decided to look at the source code for ArduCopter for ideas. Looking through the code we discovered that ArduCopter also adjusts motor speeds to target an angular velocity. We discovered that ArduCopter used something called a PID controller to accomplish this. A PID controller is a closed loop controller used to guide industrial processes. It works by adjusting a term based on the magnitude of the current error (P), the accumulation of past errors (I), and the expected future error (D). We modified our project to operate on the same principles as ArduCopter. We implemented a PID controller class and used it to control four motor corrections: one for each motor, and one for height.
There are four correction terms: frontLeftCorrection, frontRightCorrection, backCenterCorrection, and servoCorrection. These correction values are set according to axis output values.
Each output term is the value determined by the PID controller at each motor control step. These values are calculated 50 times per second. The PID contoller is fed the target angular velocity, the actual angular velocity, and the time elapsed since the last output calculation. The PID controller uses these values to calculate the next axis output. The axis outputs are roll_output, pitch_output, yaw_output, and height_output. These are factored into the motor correction terms as shown in the following table.
| Correction terms | Equation |
| Front Left | -roll_output + pitch_output/2 |
| Front Right | roll_output + pitch_output/2 |
| Back Center | -pitch_output |
| Servo | yaw_output |
The height_output is the base motor percentage. All motors are are set to the base motor percentage plus their correction term.
Fail safe
The fail safe kills all power to the motors by sending the lowest throttle position signal to the ESCs
Testing & Technical Challenges
Testing Methodologies
Phase #1
Initial testing of the Tricopter, was purely electrical. Being that all the components where purchased individually, custom wiring was needed to interconnect the components. As each component was connected and shrink tubed, continuity tests where performed to ensure no shorts existed. To power the system a variable 17AMP external power supply. By using a power supply, in place of a battery back, we where provided the ability to current limit and thus protect the various components.
Phase #2
Following the verification of the the electrical components, rudimentary flight and motor control tests began. During this phase no propellers where attached to the motors due to safety concerns. The main objective was to fully comprehend the correlation between motor speed and pulse width percentage. It was during this phase that the team encountered issues with the included PWM class. The issue and solution was documented in Issue #2.
Issue #1
The first issue encountered was related to interfacing the ESCs with the SJSU-ONE PWM driver. The PWM driver would provide a pulse-width of 5ms, thus exceeding the required 1-2ms range. To resolve this issue, the team wrote a new driver in order to preserve the 1-2ms pulse-width range. The new driver largely mimicked the provided one, however the calculation for the pulse-width was modified to:
pulseWidth = sys_get_cpu_clock() * ( (percent/100 * (MAX_PULSE - MIN_PULSE) ) + MIN_PULSE );
Issue #2
The Sunkee 10DOF IMU being a low end device, proved to be susceptible to the vibrations from the motor. This susceptibility lead to erratic measurements. To resolve this issue the motors and IMU where placed on rubber mounts. This aided in reducing the erratic measurements, however due to the severe vibrations induced by the motors additional software filtering was needed. Both the gyroscope and accelemoter data where placed through a rudimentary low-pass software filter. To further counteract system noise, a average of the calculated orientation value is computed prior to being sent to the balancing algorithm.
Issue #3
Implementation
This section includes implementation, but again, not the details, just the high level. For example, you can list the steps it takes to communicate over a sensor, or the steps needed to write a page of memory onto SPI Flash. You can include sub-sections for each of your component implementation.
Conclusion
Conclude your project here. You can recap your testing and problems. You should address the "so what" part here to indicate what you ultimately learnt from this project. How has this project increased your knowledge?
Project Video
Upload a video of your project and post the link here.
Project Source Code
Send me your zipped source code and I will upload this to SourceForge and link it for you.
References
Acknowledgement
Any acknowledgement that you may wish to provide can be included here.
References Used
- Hobby servo fundamentals http://www.princeton.edu/~mae412/TEXT/NTRAK2002/292-302.pdf
Appendix
You can list the references you used.