Difference between revisions of "Binary Search"
Proj user16 (talk | contribs) (→Binary Search) |
Proj user16 (talk | contribs) |
||
| (4 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
==Binary Search== | ==Binary Search== | ||
| − | The | + | The drawback of the linear search was that, it was not efficient enough when the data set was huge. This Drawback is eliminated when Binary Search algorithm is used. But the drawback of this algorithm is that the data set has to be sorted. |
In this Algorithm the data set would be divided into 2 equal parts in every iteration till the required element is found or till the case when further equal division is not possible. | In this Algorithm the data set would be divided into 2 equal parts in every iteration till the required element is found or till the case when further equal division is not possible. | ||
This algorithm is similar to searching for a particular page in a book. | This algorithm is similar to searching for a particular page in a book. | ||
| Line 10: | Line 10: | ||
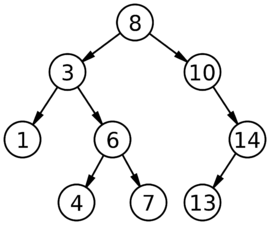
Below Image shows the formation of the algorithm in binary tree structure. | Below Image shows the formation of the algorithm in binary tree structure. | ||
[[File:CmpE243_F16_Binary Search Algorithm.png|thumb|link=File:CmpE243_F16_Binary Search Algorithm.png|frame|upright=0.9|center|Binary Search Tree]] | [[File:CmpE243_F16_Binary Search Algorithm.png|thumb|link=File:CmpE243_F16_Binary Search Algorithm.png|frame|upright=0.9|center|Binary Search Tree]] | ||
| + | |||
'''Code Snippet''' | '''Code Snippet''' | ||
| − | < | + | <syntaxhighlight lang="c"> |
#include <stdio.h> | #include <stdio.h> | ||
| Line 22: | Line 23: | ||
int first = 0, last = size - 1, middle = (first+last)/2; | int first = 0, last = size - 1, middle = (first+last)/2; | ||
| − | while (first <= last) | + | while (first <= last) //looping over the array to find the matching element till all elements in each half are compared |
{ | { | ||
| − | if (array[middle] < key) | + | if (array[middle] < key) //if element is lesser than the key value |
first = middle + 1; | first = middle + 1; | ||
| − | else if (array[middle] == key) { | + | else if (array[middle] == key) { // if matched with key |
return middle+1; | return middle+1; | ||
break; | break; | ||
| Line 32: | Line 33: | ||
else | else | ||
{ | { | ||
| − | last = middle - 1; | + | last = middle - 1; // reducing the size of the halves |
} | } | ||
| − | middle = (first + last)/2; | + | middle = (first + last)/2; //re-calculating the middle value after each iteration |
} | } | ||
return 0; | return 0; | ||
| Line 46: | Line 47: | ||
printf("Enter number of elements\n"); | printf("Enter number of elements\n"); | ||
| − | scanf("%d",&n); | + | scanf("%d",&n); // defining the array size |
| − | int array | + | int* array = (int*)malloc(n*sizeof(int)); //allocating size of the array dynamically |
printf("Enter %d integers\n", n); | printf("Enter %d integers\n", n); | ||
for (int i = 0; i < n; i++) | for (int i = 0; i < n; i++) | ||
{ | { | ||
| − | scanf("%d",&array[i]); | + | scanf("%d",&array[i]); // Setting the array elements |
} | } | ||
printf("Enter value to find\n"); | printf("Enter value to find\n"); | ||
| − | scanf("%d", &key); | + | scanf("%d", &key); // Keying in the value which has to be searched |
| − | pos= bin_search(array,n,key); | + | pos= bin_search(array,n,key); // Calling the Binary search function |
if(pos==0) | if(pos==0) | ||
{ | { | ||
| − | printf("Search unsuccessful, %d not found.\n", key); // If position of the searching stays at 0 element or beginning | + | printf("Search unsuccessful, %d not found.\n", key); // If position of the searching stays at 0 element or beginning |
} | } | ||
else | else | ||
{ | { | ||
| − | printf("%d found at location %d.\n", key, pos); | + | printf("%d found at location %d.\n", key, pos); //Printing the value fetched |
} | } | ||
return 0; | return 0; | ||
} | } | ||
| − | </ | + | </syntaxhighlight> |
Latest revision as of 22:57, 8 December 2016
Binary Search
The drawback of the linear search was that, it was not efficient enough when the data set was huge. This Drawback is eliminated when Binary Search algorithm is used. But the drawback of this algorithm is that the data set has to be sorted. In this Algorithm the data set would be divided into 2 equal parts in every iteration till the required element is found or till the case when further equal division is not possible. This algorithm is similar to searching for a particular page in a book. Say for example a book is having 20 pages and 8th page is to be found. Now equal halves of 20 page book is 0-10 pages block and 11-20 pages block. So 8th page falls under 0-10 page block. This continues for few more iterations, till 8th page is reached.
This method needs [log2n]+1 comparisons, i.e O(log n) in Big O notation, i.e. for Thousands of records, it needs about five to six comparisons, which is way better than Linear search.
Below Image shows the formation of the algorithm in binary tree structure.
Code Snippet
#include <stdio.h>
/*Binary search function to search for a key in the List*/
int bin_search(int array[],int size,int key)
{
int first = 0, last = size - 1, middle = (first+last)/2;
while (first <= last) //looping over the array to find the matching element till all elements in each half are compared
{
if (array[middle] < key) //if element is lesser than the key value
first = middle + 1;
else if (array[middle] == key) { // if matched with key
return middle+1;
break;
}
else
{
last = middle - 1; // reducing the size of the halves
}
middle = (first + last)/2; //re-calculating the middle value after each iteration
}
return 0;
}
int main()
{
int n, key, pos;
printf("Enter number of elements\n");
scanf("%d",&n); // defining the array size
int* array = (int*)malloc(n*sizeof(int)); //allocating size of the array dynamically
printf("Enter %d integers\n", n);
for (int i = 0; i < n; i++)
{
scanf("%d",&array[i]); // Setting the array elements
}
printf("Enter value to find\n");
scanf("%d", &key); // Keying in the value which has to be searched
pos= bin_search(array,n,key); // Calling the Binary search function
if(pos==0)
{
printf("Search unsuccessful, %d not found.\n", key); // If position of the searching stays at 0 element or beginning
}
else
{
printf("%d found at location %d.\n", key, pos); //Printing the value fetched
}
return 0;
}